Approximating double n-capture

We want to approximate the seqeunce \(A(n,\gamma)X(n,\gamma)B\) as \(A(nn,\gamma)B\) by combining the two successive neutron captures into a single rate, assuming equilibrium of nucleus \(X\).

This type of approximation is commonly done in the “aprox” family of networks, for example, approximating the sequence: \({}^{52}\mathrm{Fe}(n,\gamma){}^{53}\mathrm{Fe}(n,\gamma){}^{54}\mathrm{Fe}\).

import pynucastro as pyna

rl = pyna.ReacLibLibrary()

Unapproximated version

We’ll create a simple network of iron isotopes linked by neutron capture.

lib = rl.linking_nuclei(["fe52", "fe53", "fe54", "n"])

rc = pyna.PythonNetwork(libraries=[lib])
rc.write_network("ncapture.py")

import ncapture

fig = rc.plot(rotated=True, curved_edges=True)

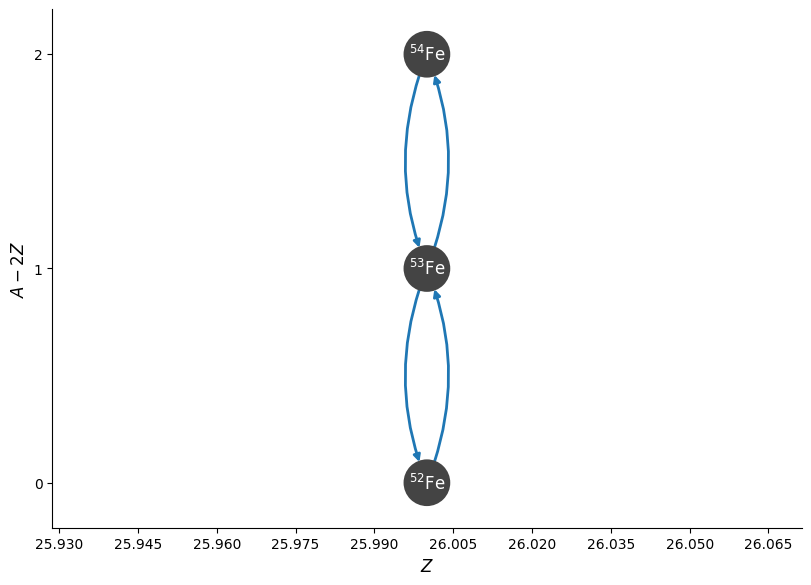
Now we’ll integrate it, starting with a mix of \({}^{52}\mathrm{Fe}\) and \(n\).

import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt

rho = 1.e9
T = 3.e9

X0 = np.zeros(ncapture.nnuc)
X0[ncapture.jn] = 0.5
X0[ncapture.jfe52] = 0.5
Y0 = X0 / ncapture.A

tmax = 1.e-5
sol = solve_ivp(ncapture.rhs, [0, tmax], Y0, method="BDF", jac=ncapture.jacobian,
                dense_output=True, args=(rho, T), rtol=1.e-6, atol=1.e-8)

fig = plt.figure()
ax = fig.add_subplot(111)

for i in range(ncapture.nnuc):
    ax.loglog(sol.t, sol.y[i,:] * ncapture.A[i], label=f"X({ncapture.names[i].capitalize()})")

ax.set_xlim(right=1.e-11)
ax.set_ylim(1.e-6, 1)

ax.legend(fontsize="small")
ax.set_xlabel("t (s)")
ax.set_ylabel("X")

Text(0, 0.5, 'X')

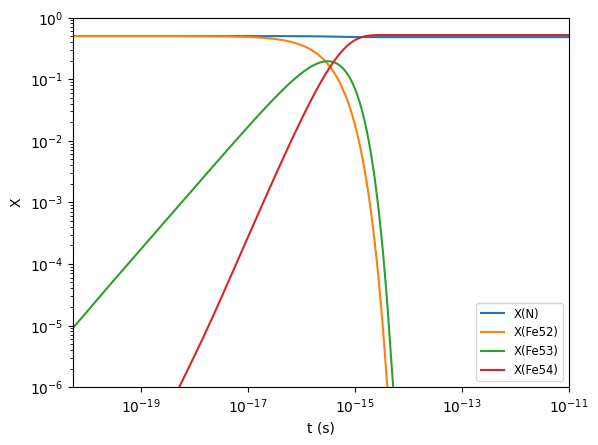
We see that the long term evolution is that all the iron winds up as \({}^{54}\mathrm{Fe}\).

Approximating the double n capture

We can use the helper function create_double_neutron_capture() to create a pair (forward and reverse) of ApproximateRates that approximate out the intermedia nucleus:

rf, rr = pyna.rates.create_double_neutron_capture(rl, pyna.Nucleus("fe52"), pyna.Nucleus("fe54"))

rf

Fe52 + n + n ⟶ Fe54 + 𝛾

We can see what rates this carries internally:

rf.hidden_rates

[Fe52 + n ⟶ Fe53 + 𝛾, Fe53 + n ⟶ Fe54 + 𝛾, Fe54 ⟶ n + Fe53, Fe53 ⟶ n + Fe52]

Tip

Alternately, we could use the make_nn_g_approx() method on the PythonNetwork once we create it.

Now we’ll build a new network with just these approximate rates:

rc2 = pyna.PythonNetwork(rates=[rf, rr])
rc2.write_network("ncapture_approx.py")

import ncapture_approx

fig = rc2.plot(rotated=True, curved_edges=True)

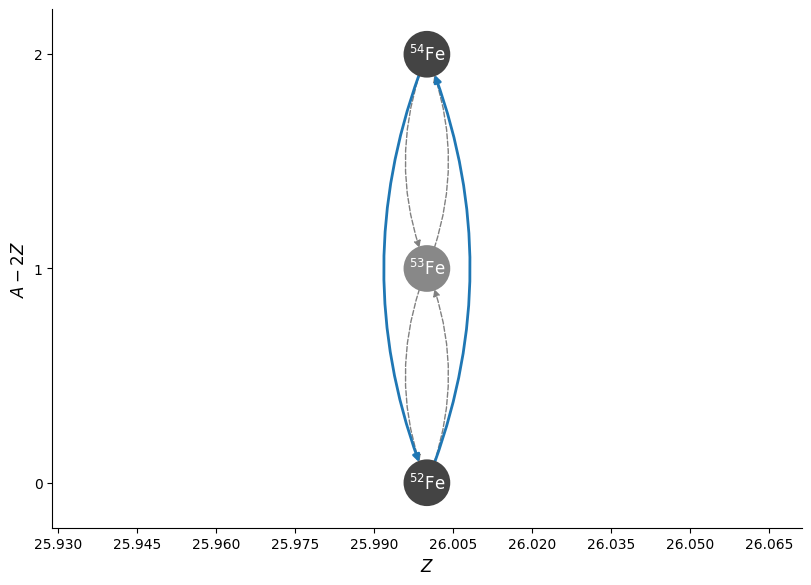
rho = 1.e9
T = 3.e9

X0 = np.zeros(ncapture_approx.nnuc)
X0[ncapture_approx.jn] = 0.5
X0[ncapture_approx.jfe52] = 0.5
Y0 = X0 / ncapture_approx.A

tmax = 1.e-5
approx_sol = solve_ivp(ncapture_approx.rhs, [0, tmax], Y0, method="BDF", jac=ncapture_approx.jacobian,
                       dense_output=True, args=(rho, T), rtol=1.e-6, atol=1.e-8)

fig = plt.figure()
ax = fig.add_subplot(111)

for i in range(ncapture_approx.nnuc):
    ax.loglog(approx_sol.t, approx_sol.y[i,:] * ncapture_approx.A[i],
              label=f"X({ncapture_approx.names[i].capitalize()})")

ax.set_xlim(right=1.e-11)
ax.set_ylim(1.e-6, 1)

ax.legend(fontsize="small")
ax.set_xlabel("t (s)")
ax.set_ylabel("X")

Text(0, 0.5, 'X')

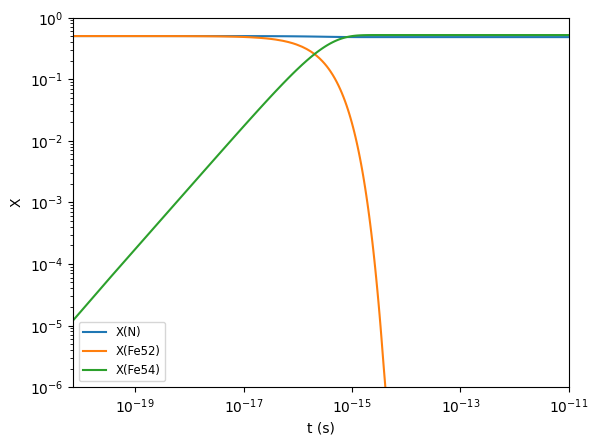
Comparison

Finally, let’s plot the nuclei in common from both nets together

fig = plt.figure()
ax = fig.add_subplot(111)

for i in range(ncapture_approx.nnuc):
    ax.loglog(approx_sol.t, approx_sol.y[i,:] * ncapture_approx.A[i],
              linestyle=":", color=f"C{i}")

    idx = ncapture.names.index(ncapture_approx.names[i])
    ax.loglog(sol.t, sol.y[idx,:] * ncapture.A[idx],
              label=f"X({ncapture.names[idx].capitalize()})",
              linestyle="-", color=f"C{i}")

ax.legend()
ax.set_xlim(right=1.e-11)
ax.set_ylim(1.e-6, 1)

(1e-06, 1)

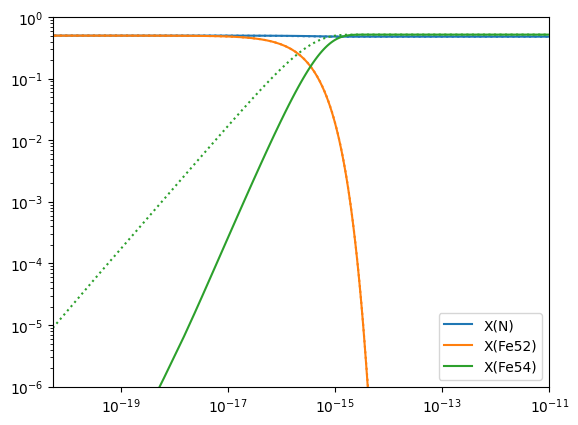
Here the dotted line is the approximate version. We see that the \({}^{52}\mathrm{Fe}\) is consumed at the same rate. The approximate net produces \({}^{54}\mathrm{Fe}\) faster simply because there is no intermediate \({}^{53}\mathrm{Fe}\) in the network.