p-p chain vs. CNO

We will explore the p-p chain and the CNO cycle to learn which rates are the slowest in each and when each dominates inside of stars.

import pynucastro as pyna

We start by getting the rates from the JINA ReacLib database. This has 80,000+ reaction rates in a standardized format.

rl = pyna.ReacLibLibrary()

Simple p-p chain

We’ll focus on the main p-p chain and get the 3 rates involved in that.

pp_rates = ["p(p,)d",
            "d(p,g)he3",
            "he3(he3,pp)he4"]
rates = rl.get_rate_by_name(pp_rates)

We can look at which rates it pulled in:

for r in rates:
    print(r)

p + p ⟶ H2 + e⁺ + 𝜈
p + p + e⁻ ⟶ H2 + 𝜈
H2 + p ⟶ He3 + 𝛾
He3 + He3 ⟶ p + p + He4

Note that ReacLib actually splits the p+p rate into two. We will add them together.

We can look at the temperature dependence of one of these rates

r = rates[0]
fig = r.plot(Tmin=1.e7, Tmax=1.e8)

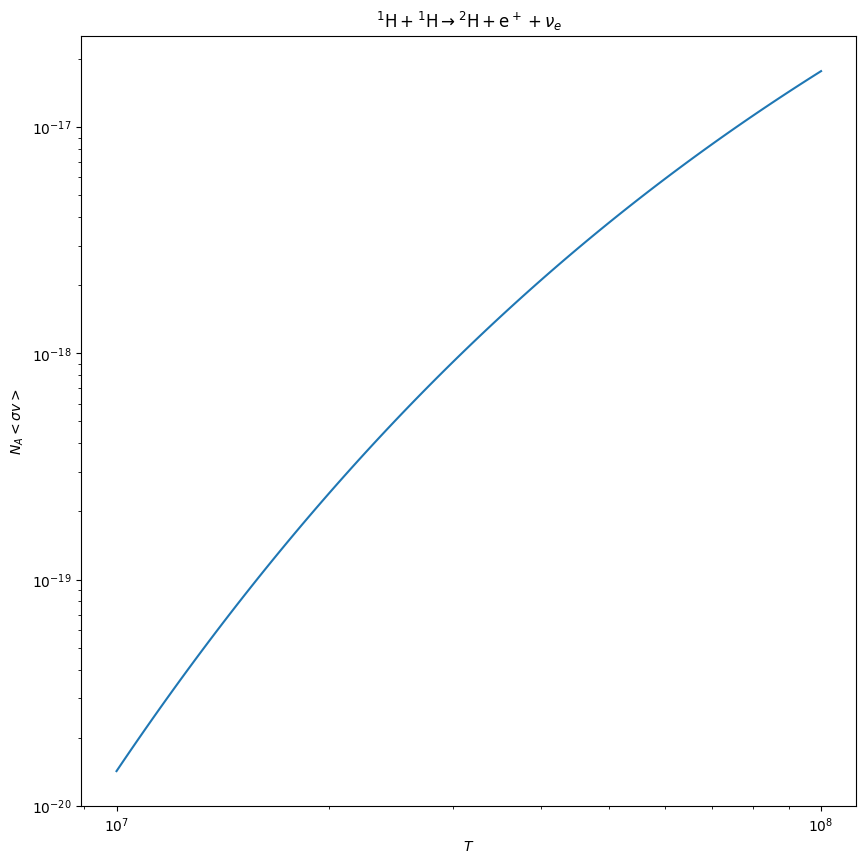
We see that it is very temperature dependent

Next we build our network (we’ll use a RateCollection) with these rates

net_pp = pyna.RateCollection(rates=rates)

We can create a thermodynamic state approximating the center of the Sun and evaluate the rates

T = 1.5e7
rho = 150
comp = pyna.Composition(net_pp.unique_nuclei)
comp.set_solar_like()

net_pp.evaluate_rates(rho, T, comp)

{p + p ⟶ H2 + e⁺ + 𝜈: 2.978374743269655e-18,
 p + p + e⁻ ⟶ H2 + 𝜈: 1.357778476769111e-20,
 H2 + p ⟶ He3 + 𝛾: 0.005874533290651895,
 He3 + He3 ⟶ p + p + He4: 1.849294558580789e-13}

We see from this that the first reaction, p + p, is by far the slowest.

fig = net_pp.plot(rho=rho, T=T, comp=comp, hide_xp=True, always_show_alpha=True)

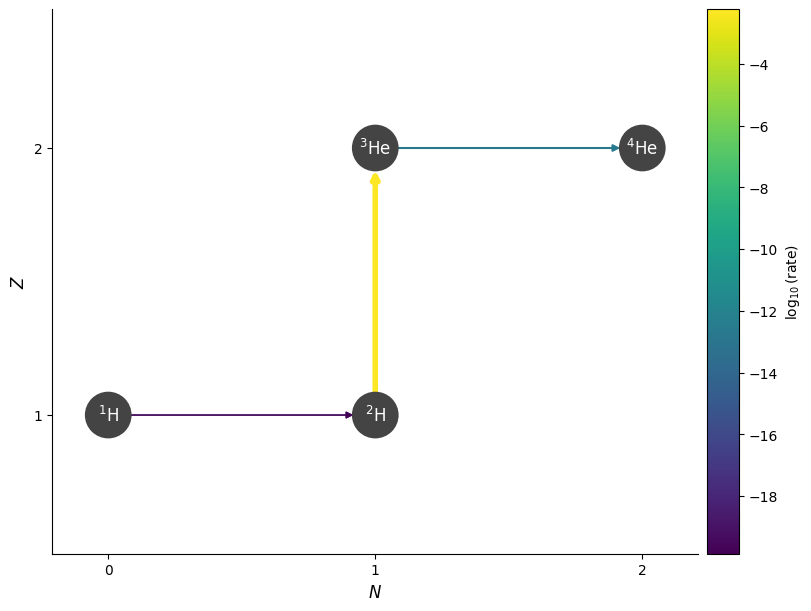
We can therefore approximate the p-p chain based on the slowest rate. If we express the rate as:

\[r = r_0 \left (\frac{T}{T_0}\right )^\nu\]

then we can find the exponent \(\nu\) about some temperature \(T_0\)

r_pp = net_pp.get_rate_by_name("p(p,)d")[0]
T0 = 1.5e7
r_pp.get_rate_exponent(T0)

3.9735120801889896

Around the conditions in the Sun, the p-p chain has a temperature dependence of \(\sim T^4\)

CNO

Now we consider the main CNO cycle. This involves 6 rates

cno_rates = ["c12(p,g)n13",
             "c13(p,g)n14",
             "n13(,)c13",
             "n14(p,g)o15",
             "n15(p,a)c12",
             "o15(,)n15"]
rates = rl.get_rate_by_name(cno_rates)

for r in rates:
    print(r)

C12 + p ⟶ N13 + 𝛾
C13 + p ⟶ N14 + 𝛾
N13 ⟶ C13 + e⁺ + 𝜈
N14 + p ⟶ O15 + 𝛾
N15 + p ⟶ He4 + C12
O15 ⟶ N15 + e⁺ + 𝜈

net_cno = pyna.RateCollection(rates=rates)

comp = pyna.Composition(net_cno.unique_nuclei)
comp.set_solar_like()

Again we can look evaluate each of the rates:

net_cno.evaluate_rates(rho, T, comp)

{C12 + p ⟶ N13 + 𝛾: 1.0467759242295144e-17,
 C13 + p ⟶ N14 + 𝛾: 3.176211597339995e-17,
 N13 ⟶ C13 + e⁺ + 𝜈: 2.9720852738029567e-07,
 N14 + p ⟶ O15 + 𝛾: 1.7295781984662848e-20,
 N15 + p ⟶ He4 + C12: 6.954822248932605e-16,
 O15 ⟶ N15 + e⁺ + 𝜈: 1.2625681768893481e-06}

Now we see that the \({}^{14}\mathrm{N}(p,\gamma){}^{15}\mathrm{O}\) rate is the slowest.

r_cno = net_cno.get_rate_by_name("n14(p,g)o15")

This is a much steeper function of temperature. Let’s explore the temperature dependence around a few points

for T in [1.e7, 2.e7, 3.e7, 4.e7]:
    print(f"T = {T}, nu = {r_cno.get_rate_exponent(T):8.5f}")

T = 10000000.0, nu = 22.82962
T = 20000000.0, nu = 17.96637
T = 30000000.0, nu = 15.60186
T = 40000000.0, nu = 14.11535

So it varies from \(T^{23}\) to \(T^{14}\) in a temperature range that includes the Sun’s core.

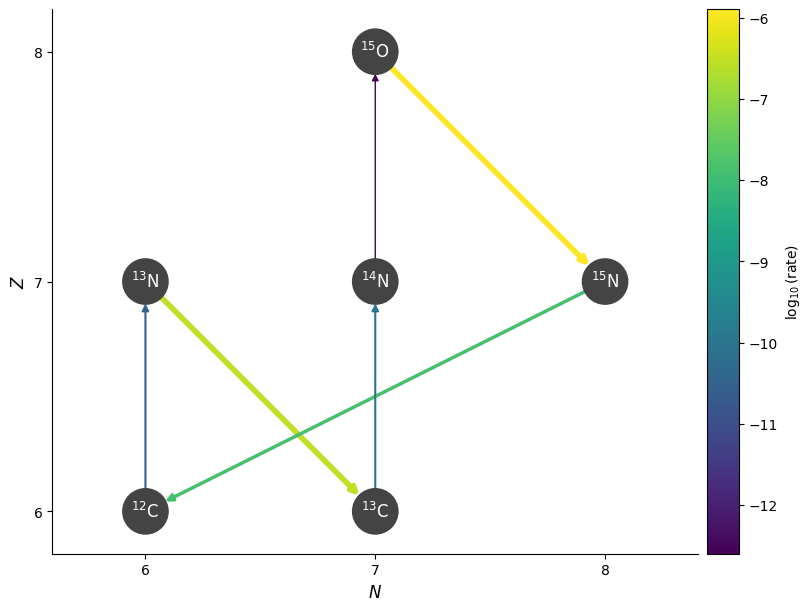
Here’s what the CNO cycle looks like

fig = net_cno.plot(rho=rho, T=T, comp=comp, hide_xp=True)

Ignoring fixed x limits to fulfill fixed data aspect with adjustable data limits.

Comparing p-p vs. CNO

The temperature dependence suggests that if the temperature were a little higher, then CNO would go faster then p-p. We can plot the two rate-limiting rates on the same axes

import numpy as np
import matplotlib.pyplot as plt

Ts = np.logspace(6.8, 8, 50)

fig, ax = plt.subplots()

ax.loglog(Ts, [r_pp.eval(q) for q in Ts], label="p-p")
ax.loglog(Ts, [r_cno.eval(q) for q in Ts], label="CNO")
ax.set_xlabel("T")
ax.set_ylabel(r"$N_A\langle \sigma v \rangle$")
ax.grid(linestyle=":", which="both")
leg = ax.legend()

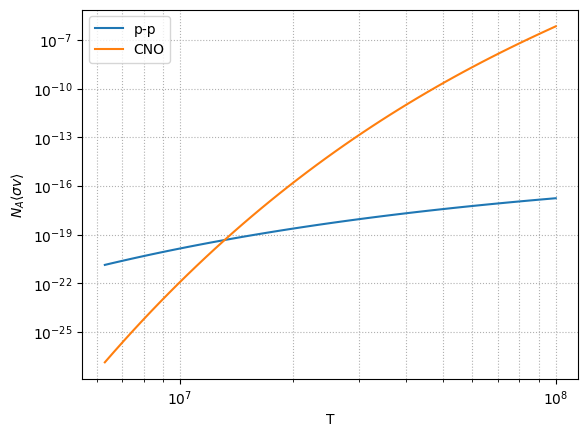
Notice that they cross over at a temperature just hotter than the Sun’s core. This means that stars more massive than the Sun (actually, about \(1.5~M_\odot\)) are powered by CNO and less massive stars are powered by p-p. The strong \(T\) dependence of CNO will play a role in determining the structure of those more massive stars.