Computing the Screened Triple-alpha rate

Computing the Screened Triple-alpha rate#

We want to evaluate the 3-\(\alpha\) rate with screening to understand how temperature sensitive it is. We’ll do this 2 different ways (but both will get the same answer).

import pynucastro as pyna

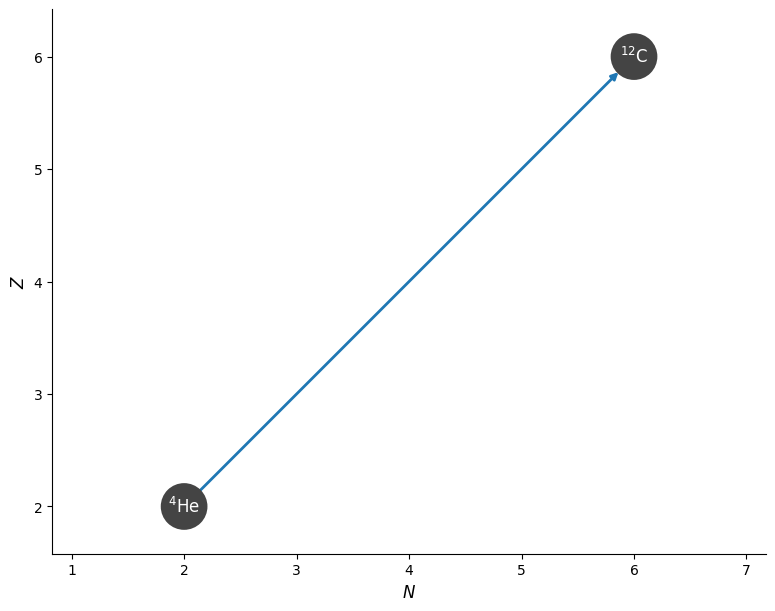
We’ll define the thermodynamics first – a composition of just He and C

temp = 1.e8
dens = 1.e6

he4 = pyna.Nucleus("he4")
c12 = pyna.Nucleus("c12")

nuclei = [he4, c12]
comp = pyna.Composition(nuclei)
comp.X[he4] = 0.9
comp.X[c12] = 0.1

fig = comp.plot()
../_images/3aaaa480e309db6e4a345455a802f37695dddccdc2ffac17cbd7f57ecca7e04e.png

Manual method#

Here well read in this rate and compute the screening factors ourselves and then build up the full form of the rate

rl = pyna.ReacLibLibrary()

triple_alpha = rl.get_rate_by_name("a(aa,)c12")

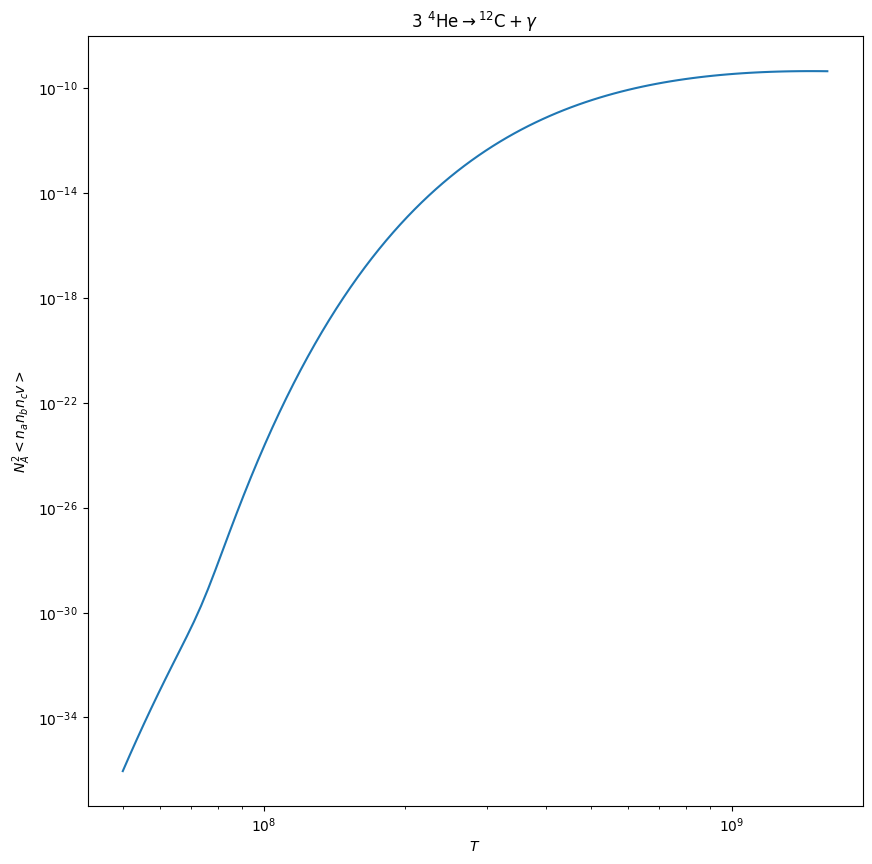
Here’s the temperature sensitivity of just the 3-\(\alpha\) rate

fig = triple_alpha.plot(Tmin=5.e7)
../_images/dafdc41477d8e494770366bd19f09b8dc6965d8434c72cb08015336a7a9fa277.png

To compute the screening, we first need to get the plasma state

plasma = pyna.make_plasma_state(temp, dens, comp.get_molar())

Now, the 3-\(\alpha\) rate requires 2 separate screening terms, first \(\alpha + \alpha\) and then \(\alpha + {}^8\mathrm{Be}\)

scn_fac1 = pyna.make_screen_factors(he4, he4)
scn1 = pyna.screening.screen5(plasma, scn_fac1)

scn_fac2 = pyna.make_screen_factors(he4, pyna.Nucleus("be8"))
scn2 = pyna.screening.screen5(plasma, scn_fac2)

scn = scn1 * scn2
print(f"{scn:20.10g}")

         5.802207275

This shows that our our thermodynamic conditions, screening speeds up the rate by almost \(6\times\).

Now, the total rate is:

\[r = f \rho^2 [Y({}^4\mathrm{He})]^3 \frac{N_A^2 \langle \sigma v \rangle}{3!}\]

where \(f\) is the screening factor and the \(3!\) is because there are 3 identical particles appearing in the reation.

We get \(N_A^2 \langle \sigma v \rangle\) by evaluating the temperature sensitivity of the rate from ReacLib.

r = scn * dens**2 / 6.0 * comp.get_molar()[he4]**3 * triple_alpha.eval(temp)
print(f"{r:20.10g}")

     2.247437735e-14

This is the rate in units of \(\mathrm{cm}^{-3}~\mathrm{s}^{-1}\)

Computing it via a RateCollection#

We can build a simple RateCollection containing only this rate

rc = pyna.RateCollection(rates=[triple_alpha])
fig = rc.plot()
../_images/4da430255e633c18a3ad49e7328bac619411d938b49d9bc739c527b000944b9e.png

The evaluate_rates() method will take the thermodynamic state and screening function (optionally) and compute the value of each of the rates in the network.

rc.evaluate_rates(dens, temp, comp, screen_func=pyna.screening.screen5)

{3 He4 ⟶ C12 + 𝛾: 2.2474377346294803e-14}

We see that we get the same value as computing it manually.

Contents