Nuclear Properties#
Here we explore how to access some of the nuclear properties from a Nucleus object.
Note
pynucastro gets the nuclear data from the Nubase 2020 compilation, which uses the CODATA 2018
constants. To be consistent, the CODATA 2018 values of the atomic mass unit and neutron
mass are provided in pynucastro.constants as constants.m_u_MeV_C18 and constants.m_n_MeV_C18
from pynucastro import Nucleus
from math import exp
Nucleus#
The Nucleus class manages all of the properties of a nucleus. We create a Nucleus simply by giving the name of the isotope
he4 = Nucleus("he4")
Tip
Nuclei names are case-insensitive and the atomic weight can come before or after the element name. All of these are equivalent:
Nucleus("ni56")
Nucleus("Ni56")
Nucleus("56ni")
From this we can access the member data:
Z,N,A: the atomic number, neutron number, and atomic massmass: the mass of the nucleus in MeVdm: the mass excess of the nucleus in MeVnucbind: the nuclear binding energy of the nucleus in MeV / nucleonA_nuc: the mass number of the nucleus (mass/ atomic mass unit)tau: the halflife of the nucleus (in seconds)
he4.Z, he4.A
(2, 4)
he4.nucbind
7.073915614499924
ni56 = Nucleus("ni56")
ni56.tau
524880.0
ni56.spin_states
1
We can also look at a summary:
ni56.summary()
Ni56 / nickel-56
----------------
A: 56
N: 28
Z: 28
mass: 52109.76214 MeV
mass excess: -53.90760 MeV
binding energy / nucleon: 8.64278 MeV
half-life: 524880.0 s
partition function: available
spin states: 1
dummy: False
nse: False
spin states are reliable: True
Tip
The helper function get_nuclei_in_range can
be used to get a list of nuclei in a range based on \(Z\), \(A\) or neutron excess,
Nucleus math#
We can also create a Nucleus via addition and subtraction operations.
c12 = Nucleus("c12")
p = Nucleus("p")
n13 = c12 + p
n13
N13
n13.mass
12114.76881146
c12 - p
B11
Exploring properties#
Let’s look at some nuclei and look at their mass excess, mass, and binding energies
p = Nucleus("p")
n = Nucleus("n")
c12 = Nucleus("c12")
ne22 = Nucleus("ne22")
ti43 = Nucleus("ti43")
fe56 = Nucleus("fe56")
for nuc in [p, n, c12, ne22, ti43, fe56]:
print(f"{str(nuc):6} {nuc.dm:15.8} {nuc.mass:15.8f} {nuc.nucbind:15.8f}")
p 7.2889711 938.78307348 0.00000000
n 8.0713181 939.56542052 0.00000000
C12 0.0 11177.92922904 7.68014458
Ne22 -8.024716 20484.84553724 8.08046563
Ti43 -29.316 40024.93040406 8.35281497
Fe56 -60.60716 52103.06257552 8.79035626
We see that the binding energy for protons and neutrons are zero, as expected.
We also see:
For \({}^{12}\mathrm{C}\) the binding energy compares well with the tablulated version from the rounded AME 2020 of
7680.145.For \({}^{22}\mathrm{Ne}\) the binding energy compares well with the tablulated version from the rounded AME 2020 of
8080.466.For \({}^{43}\mathrm{Ti}\) the binding energy compares well with the tablulated version from the rounded AME 2020 of
8352.81.For \({}^{56}\mathrm{Fe}\) the binding energy compares well with the tablulated version from the rounded AME 2020 of
8790.356.
from pynucastro.constants import constants
We also see that the mass of \({}^{12}\mathrm{C}\) agrees with the atomic mass unit from the CODATA compilation:
c12.mass / 12 - constants.m_u_MeV_C18
1.1368683772161603e-13
Let’s look at a less common nucleus. From Nubase 2020 data, the spin for \({}^{61}\mathrm{Fe}\) is determined experimentally but the argument to determine it was judged to be weak. We are able to choose whether to use these unreliable spin data or omit them.
fe61 = Nucleus("fe61")
if fe61.spin_reliable:
print(f"{str(fe61)}: {fe61.spin_states} spin states")
else:
print(f"{str(fe61)}: {fe61.spin_states} spin states (not strongly experimentally substantiated. Consider dropping {str(fe61)} from your network.)")
Fe61: 4 spin states (not strongly experimentally substantiated. Consider dropping Fe61 from your network.)
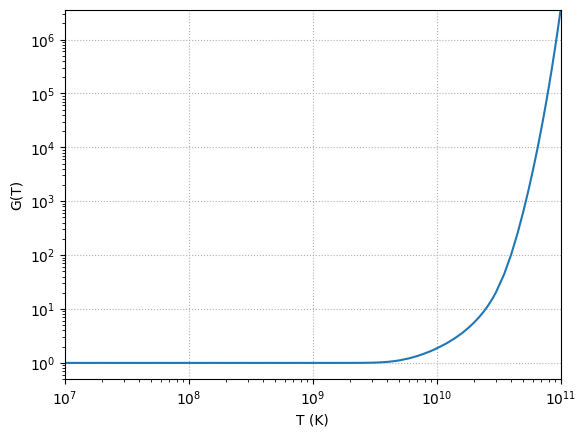
Partition functions#
Nucleus objects also have their partition function data (managed by PartitionFunction. These come from the work of Rauscher et al. [1997] for low temperatures (\(T \le 10^{10}~\mathrm{K}\)) and Rauscher [2003] for high temperatures. The data from these two sources is concatenated and a spline fit is used to evaluate it.
We can use eval to evaluate the partition function at any temperature.
Note
eval gives log(partition function). To get the actual partition function, you would need to do exp() afterwards
ne20 = Nucleus("ne20")
exp(ne20.partition_function.eval(4.e9))
1.043747
And we can also plot it vs. temperature.
fig = ne20.partition_function.plot()