pynucastro usage examples#
This notebook illustrates some of the higher-level data structures in pynucastro.
import pynucastro as pyna
Examining a single rate#
There are several ways to load a single rate. If you down load the specific rate file from the JINA ReacLib website, then you can load the rate via load_rate() and
just giving that file name, e.g.,
c13pg = pyna.load_rate("c13-pg-n14-nacr")
However, an easier way to do this is to pass in the shorthand name for the rate to a library.
Here we’ll read in the entire ReacLib library
and get the \({}^{12}\mathrm{C}(\alpha,\gamma){}^{16}\mathrm{O}\) rate. The result will be a Rate object (or an object of a class derived from Rate). There are a lot of methods in the Rate class that allow you to explore the rate.
rl = pyna.ReacLibLibrary()
c13pg = rl.get_rate_by_name("c13(p,g)n14")
A Rate can display itself nicely
c13pg
C13 + p ⟶ N14 + 𝛾
The original reaclib source#
we can easily see the original source from ReacLib
print(c13pg.original_source)
4
p c13 n14 nacrr 7.55100e+00
1.518250e+01-1.355430e+01 0.000000e+00 0.000000e+00
0.000000e+00 0.000000e+00-1.500000e+00
4
p c13 n14 nacrn 7.55100e+00
1.851550e+01 0.000000e+00-1.372000e+01-4.500180e-01
3.708230e+00-1.705450e+00-6.666670e-01
4
p c13 n14 nacrr 7.55100e+00
1.396370e+01-5.781470e+00 0.000000e+00-1.967030e-01
1.421260e-01-2.389120e-02-1.500000e+00
This is a rate that consists of 3 sets, each of which has 7 coefficients in a form:
Reference for the rate#
We can find the reference in the literature that provided the rate (if available)
c13pg.source
{'Label': 'nacr',
'Author': 'Angulo C.',
'Title': 'A compilation of charged-particle induced thermonuclear reaction rates',
'Publisher': 'Nuclear Physics, A656, 3-183',
'Year': '1999',
'URL': 'https://reaclib.jinaweb.org/labels.php?action=viewLabel&label=nacr'}
Evaluating the rate#
Our rate is just temperature dependent portion of the rate, usually expressed as \(N_A \langle \sigma v \rangle\). We can evaluate this for a given temperature (in K) easily:
c13pg.eval(1.e9)
3883.4778216250666
Nuclei involved#
The nuclei involved are all Nucleus objects. They have members Z and N that give the proton and neutron number
print(c13pg.reactants)
print(c13pg.products)
[p, C13]
[N14]
r2 = c13pg.reactants[1]
Note
Each of the nuclei are a pynucastro Nucleus type
type(r2)
pynucastro.nucdata.nucleus.Nucleus
print(r2.Z, r2.N)
6 7
Temperature sensitivity#
We can find the temperature sensitivity about some reference temperature. This is the exponent when we write the rate as
We can estimate this given a reference temperature, \(T_0\)
c13pg.get_rate_exponent(2.e7)
16.21089670710968
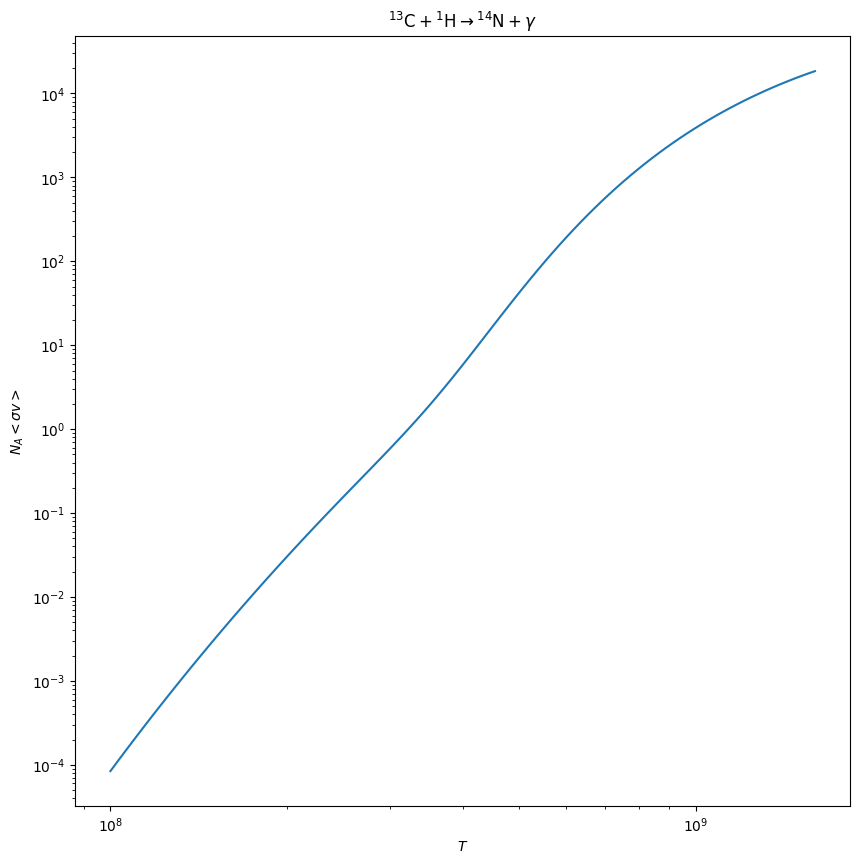
Plot the rate’s temperature dependence#
A reaction rate has a complex temperature dependence that is defined in the reaclib files. The plot() method will plot this for us
fig = c13pg.plot()
Density dependence#
A rate also knows its density dependence – this is inferred from the reactants in the rate description and is used to construct the terms needed to write a reaction network. Note: since we want reaction rates per gram, this number is 1 less than the number of nuclei
c13pg.dens_exp
1
Working with a group of rates#
A RateCollection() class allows us to work with a group of rates. This is used to explore their relationship. Other classes (introduced soon) are built on this and will allow us to output network code directly.
Here we create a list with some of the individual rates in the ReacLib library
rate_names = ["c12(p,g)n13",
"c13(p,g)n14",
"n13(,)c13",
"n13(p,g)o14",
"n14(p,g)o15",
"n15(p,a)c12",
"o14(,)n14",
"o15(,)n15"]
rates = rl.get_rate_by_name(rate_names)
rc = pyna.RateCollection(rates=rates)
Printing a rate collection shows all the rates
print(rc)
C12 + p ⟶ N13 + 𝛾
C13 + p ⟶ N14 + 𝛾
N13 ⟶ C13 + e⁺ + 𝜈
N13 + p ⟶ O14 + 𝛾
N14 + p ⟶ O15 + 𝛾
N15 + p ⟶ He4 + C12
O14 ⟶ N14 + e⁺ + 𝜈
O15 ⟶ N15 + e⁺ + 𝜈
More detailed information is provided by network_overview()
print(rc.network_overview())
p
consumed by:
C12 + p ⟶ N13 + 𝛾
C13 + p ⟶ N14 + 𝛾
N13 + p ⟶ O14 + 𝛾
N14 + p ⟶ O15 + 𝛾
N15 + p ⟶ He4 + C12
produced by:
He4
consumed by:
produced by:
N15 + p ⟶ He4 + C12
C12
consumed by:
C12 + p ⟶ N13 + 𝛾
produced by:
N15 + p ⟶ He4 + C12
C13
consumed by:
C13 + p ⟶ N14 + 𝛾
produced by:
N13 ⟶ C13 + e⁺ + 𝜈
N13
consumed by:
N13 ⟶ C13 + e⁺ + 𝜈
N13 + p ⟶ O14 + 𝛾
produced by:
C12 + p ⟶ N13 + 𝛾
N14
consumed by:
N14 + p ⟶ O15 + 𝛾
produced by:
C13 + p ⟶ N14 + 𝛾
O14 ⟶ N14 + e⁺ + 𝜈
N15
consumed by:
N15 + p ⟶ He4 + C12
produced by:
O15 ⟶ N15 + e⁺ + 𝜈
O14
consumed by:
O14 ⟶ N14 + e⁺ + 𝜈
produced by:
N13 + p ⟶ O14 + 𝛾
O15
consumed by:
O15 ⟶ N15 + e⁺ + 𝜈
produced by:
N14 + p ⟶ O15 + 𝛾
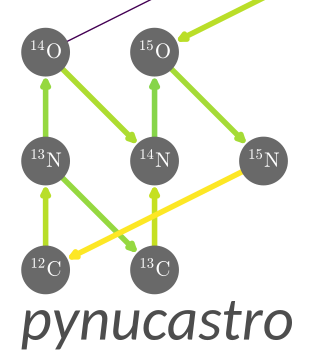
Show a network diagram#
We visualize the network using NetworkX.
Note
By default, the network plot does not show H or He unless we have H + H or triple-\(\alpha\) reactions in the network. This is intended to reduce clutter.
fig = rc.plot()
Ignoring fixed x limits to fulfill fixed data aspect with adjustable data limits.
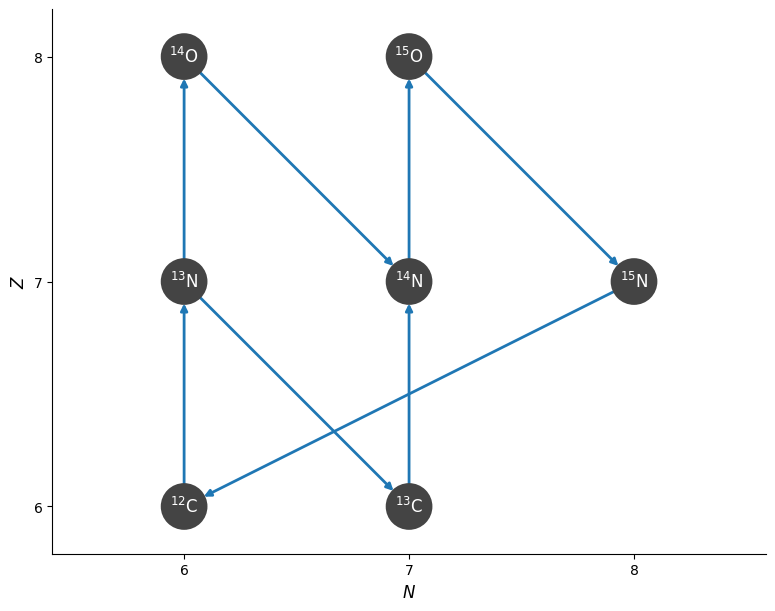
There are many options that can be used to configure this plot, for instance, creating a rotated version (useful for very large nets).
Evaluate the rates#
To evaluate the rates in a network, we need a composition, which is managed via a Composition object.
comp = pyna.Composition(rc.get_nuclei())
comp.set_solar_like()
We can then pick a density and temperature and evaluate all of the rates in the network
rho = 1.e4
T = 1.e8
rc.evaluate_rates(rho, T, comp)
{C12 + p ⟶ N13 + 𝛾: 4.3825344233265836e-05,
C13 + p ⟶ N14 + 𝛾: 0.00012943869407433363,
N13 ⟶ C13 + e⁺ + 𝜈: 2.547501663259677e-07,
N13 + p ⟶ O14 + 𝛾: 4.851762091044591e-06,
N14 + p ⟶ O15 + 𝛾: 9.813707457231503e-07,
N15 + p ⟶ He4 + C12: 0.0875185522576593,
O14 ⟶ N14 + e⁺ + 𝜈: 2.003669148162566e-06,
O15 ⟶ N15 + e⁺ + 𝜈: 1.0822012944765842e-06}
Explore the network’s rates#
We can also interactively explore the rates in a notebook using Jupyter widgets.
Interactive exploration is enabled through the Explorer class, which takes a RateCollection and a Composition
re = pyna.Explorer(rc, comp)
re.explore()