Example of Integrating a Network

Creating a Network

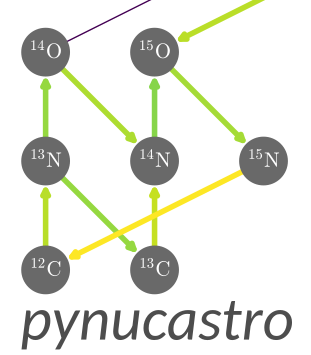
We will start by looking at the CNO network for simplicity. We will first need to import pynucastro, read through the ReacLib library, and pass in the names of the reaction rates we are interested in.

import pynucastro as pyna
rl = pyna.ReacLibLibrary()
rate_names = ["c12(p,g)n13",
              "c13(p,g)n14",
              "n13(,)c13",
              "n13(p,g)o14",
              "n15(p,a)c12",
              "o14(,)n14",
              "o15(,)n15"]

rates = rl.get_rate_by_name(rate_names)
rates

[C12 + p ⟶ N13 + 𝛾,
 C13 + p ⟶ N14 + 𝛾,
 N13 ⟶ C13 + e⁺ + 𝜈,
 N13 + p ⟶ O14 + 𝛾,
 N15 + p ⟶ He4 + C12,
 O14 ⟶ N14 + e⁺ + 𝜈,
 O15 ⟶ N15 + e⁺ + 𝜈]

PythonNetwork has methods to write the RHS of the system of ODEs.

pynet = pyna.PythonNetwork(rates=rates)

The write_network() method outputs the Python code that is used to define the RHS for integration to a file you choose.

pynet.write_network("cno_test_integrate.py")

Integrating a Network

There are a wide variety of ODE integration solvers within the Julia DifferentialEquation package. They can be located at the DifferentialEquation.jl docs along with other useful information about the package.

import numba
import numpy as np
from diffeqpy import de
import cno_test_integrate as cno #importing network created

---------------------------------------------------------------------------
ModuleNotFoundError                       Traceback (most recent call last)
Cell In[4], line 3
      1 import numba
      2 import numpy as np
----> 3 from diffeqpy import de
      4 import cno_test_integrate as cno #importing network created

ModuleNotFoundError: No module named 'diffeqpy'

After importing all the necessary libraries and modules, we can initialize the thermodynamic conditions, initial compositions, the time span, and the algorithm or method we will be using to solve with.

rho = 150. #g/cm^3
T = 1.5e7  #K
screen_func = None

Y0 = np.zeros((cno.nnuc), dtype=np.float64) # Initialize array of mass fractions

Y0[cno.jp] = 0.7 #Solar mix of mass fractions
Y0[cno.jhe4] = 0.28
Y0[cno.jc12] = 0.02

Y0[:] = Y0[:]/cno.A[:] #Converting to molar fractions

tspan = (0.0, 1.e20) 
p = np.array([rho, T]) #Array of initial parameters
alg = de.FBDF() #Choosing integration method

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[5], line 5
      2 T = 1.5e7  #K
      3 screen_func = None
----> 5 Y0 = np.zeros((cno.nnuc), dtype=np.float64) # Initialize array of mass fractions
      7 Y0[cno.jp] = 0.7 #Solar mix of mass fractions
      8 Y0[cno.jhe4] = 0.28

NameError: name 'cno' is not defined

We can then write the functions to return the jacobian and the RHS of the Differential Equations. Numba can be used to do just-in-time compilation of the functions to speed up the code.

def f(u, p, t): #u = array of unknowns, p = array of parameters, t = array of time
   rho, T = p
   Y = u
   return cno.rhs_eq(t, Y, rho, T, None) #calling RHS 

def f_jac(u, p, t):
   rho, T = p
   Y = u
   return cno.jacobian_eq(t, Y, rho, T, None) #Calling Jacobian

numba_f = numba.njit(f) #Using Numba on functions
numba_jac = numba.njit(f_jac)

ff = de.ODEFunction(numba_f, jac=numba_jac)

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[6], line 14
     11 numba_f = numba.njit(f) #Using Numba on functions
     12 numba_jac = numba.njit(f_jac)
---> 14 ff = de.ODEFunction(numba_f, jac=numba_jac)

NameError: name 'de' is not defined

We combine the function f(u, p, t) and f_jac(u, p, t) into a single variable ff. The reason for this is because the first parameter in de.ODEProblem() must be a single variable calling the functions.

prob = de.ODEProblem(ff, Y0, tspan, p)
sol = de.solve(prob, alg, abstol=1.e-9, reltol=1.e-9)

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[7], line 1
----> 1 prob = de.ODEProblem(ff, Y0, tspan, p)
      2 sol = de.solve(prob, alg, abstol=1.e-9, reltol=1.e-9)

NameError: name 'de' is not defined

For more information on ODE Problems visit DifferentialEquation.jl docs

Printing and Plotting

It is useful to be able to print and plot certain things to gain a better understanding of what is going on with the solver method and the reactions. Below are useful print statements to help you understand what is going on behind the scenes.

print(sol.retcode) #Tells you if it successfully solved 

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[8], line 1
----> 1 print(sol.retcode) #Tells you if it successfully solved 

NameError: name 'sol' is not defined

print(sol.stats) #Gives statistics on what the solver did

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[9], line 1
----> 1 print(sol.stats) #Gives statistics on what the solver did

NameError: name 'sol' is not defined

print("Final Y =", sol.u[-1]) #prints out final molar fractions

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[10], line 1
----> 1 print("Final Y =", sol.u[-1]) #prints out final molar fractions

NameError: name 'sol' is not defined

import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)

t_dense = np.geomspace(1e1, tspan[-1], num=1000)
species = sol(t_dense)

for i in range(cno.nnuc):
    ax.loglog(t_dense, species[i], label=f"X({cno.names[i].capitalize()})")

#ax.set_xlim(1.e1, 1.e6)
ax.set_ylim(1.e-15, 1.0)
ax.legend(fontsize="small")
ax.set_xlabel("t (s)")
ax.set_ylabel("X")

fig.set_size_inches((8, 6))

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[11], line 5
      2 fig = plt.figure()
      3 ax = fig.add_subplot(111)
----> 5 t_dense = np.geomspace(1e1, tspan[-1], num=1000)
      6 species = sol(t_dense)
      8 for i in range(cno.nnuc):

NameError: name 'tspan' is not defined