Example of integrating a network#
This notebook illustrates how to create a python network and integrate it with the scipy library.
import pynucastro as pyna
We’ll start again with the basic CNO network explored earlier. Again, we’ll read in the entire ReacLib library
and pass in the names of the rates in the form of a string A(x,y)B to filter out just the rates we are interested in.
rl = pyna.ReacLibLibrary()
rate_names = ["c12(p,g)n13",
"c13(p,g)n14",
"n13(,)c13",
"n13(p,g)o14",
"n14(p,g)o15",
"n15(p,a)c12",
"o14(,)n14",
"o15(,)n15"]
rates = rl.get_rate_by_name(rate_names)
rates
[C12 + p ⟶ N13 + 𝛾,
C13 + p ⟶ N14 + 𝛾,
N13 ⟶ C13 + e⁺ + 𝜈,
N13 + p ⟶ O14 + 𝛾,
N14 + p ⟶ O15 + 𝛾,
N15 + p ⟶ He4 + C12,
O14 ⟶ N14 + e⁺ + 𝜈,
O15 ⟶ N15 + e⁺ + 𝜈]
A PythonNetwork is based on a RateCollection but has methods to write the RHS of the system of ODEs.
pynet = pyna.PythonNetwork(rates=rates)
fig = pynet.plot()
Ignoring fixed x limits to fulfill fixed data aspect with adjustable data limits.
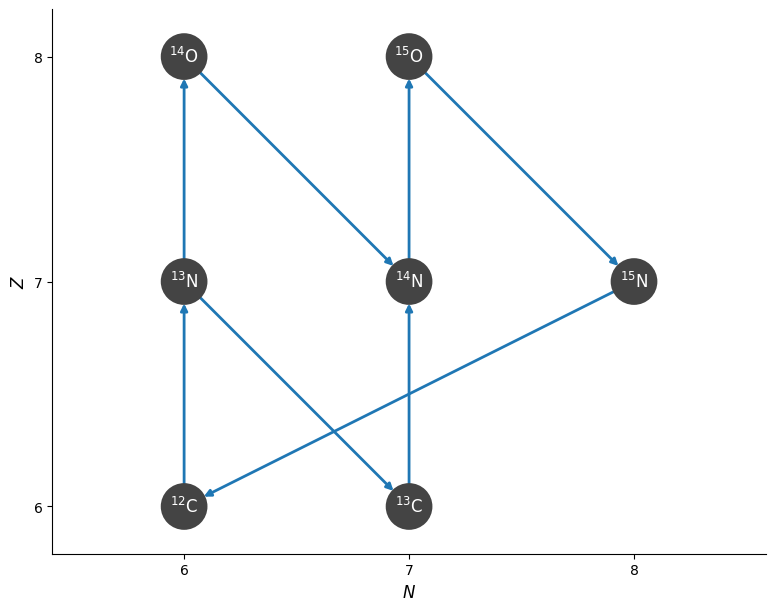
For example, this network knows how to write the full term for a reaction that goes into the \(dY/dt\) equation of the ODE system.
Here we pick one of the rates that is part of the network an explore it.
r = pynet.rates[1]
print(r)
C13 + p ⟶ N14 + 𝛾
a rate also knows what its contribution is to the \(dY/dt\) equation is:
print(r.ydot_string_py())
rho*Y[jp]*Y[jc13]*rate_eval.p_C13__N14
and the code needed to evaluate that rate (the T-dependent part) is output by the Rate class:
print(r.function_string_py())
@numba.njit()
def p_C13__N14(rate_eval, tf):
# C13 + p --> N14
rate = 0.0
# nacrr
rate += np.exp( 15.1825 + -13.5543*tf.T9i
+ -1.5*tf.lnT9)
# nacrn
rate += np.exp( 18.5155 + -13.72*tf.T913i + -0.450018*tf.T913
+ 3.70823*tf.T9 + -1.70545*tf.T953 + -0.666667*tf.lnT9)
# nacrr
rate += np.exp( 13.9637 + -5.78147*tf.T9i + -0.196703*tf.T913
+ 0.142126*tf.T9 + -0.0238912*tf.T953 + -1.5*tf.lnT9)
rate_eval.p_C13__N14 = rate
Note
The temperature-dependent rate evaluation functions take a Tfactor object, which precomputes most of the commonly-used temperature factors in the rates.
The write_network() method will output the python code needed to define the RHS of a network for integration with the SciPy integrators.
Since python code can be slow, we use Numba to do just-in-time compilation of the functions to speed things up.
pynet.write_network("cno_test_integrate.py")
%cat cno_test_integrate.py
import numba
import numpy as np
from scipy import constants
from numba.experimental import jitclass
from pynucastro.rates import TableIndex, TableInterpolator, TabularRate, Tfactors
from pynucastro.screening import PlasmaState, ScreenFactors
jp = 0
jhe4 = 1
jc12 = 2
jc13 = 3
jn13 = 4
jn14 = 5
jn15 = 6
jo14 = 7
jo15 = 8
nnuc = 9
A = np.zeros((nnuc), dtype=np.int32)
A[jp] = 1
A[jhe4] = 4
A[jc12] = 12
A[jc13] = 13
A[jn13] = 13
A[jn14] = 14
A[jn15] = 15
A[jo14] = 14
A[jo15] = 15
Z = np.zeros((nnuc), dtype=np.int32)
Z[jp] = 1
Z[jhe4] = 2
Z[jc12] = 6
Z[jc13] = 6
Z[jn13] = 7
Z[jn14] = 7
Z[jn15] = 7
Z[jo14] = 8
Z[jo15] = 8
# masses in ergs
mass = np.zeros((nnuc), dtype=np.float64)
mass[jp] = 0.0015040963047307696
mass[jhe4] = 0.0059735574859708365
mass[jc12] = 0.017909017027273523
mass[jc13] = 0.01940644192976114
mass[jn13] = 0.01940999951603316
mass[jn14] = 0.020898440897976135
mass[jn15] = 0.022386433805845516
mass[jo14] = 0.020906683078094165
mass[jo15] = 0.02239084645968795
names = []
names.append("H1")
names.append("He4")
names.append("C12")
names.append("C13")
names.append("N13")
names.append("N14")
names.append("N15")
names.append("O14")
names.append("O15")
def to_composition(Y):
"""Convert an array of molar fractions to a Composition object."""
from pynucastro import Composition, Nucleus
nuclei = [Nucleus.from_cache(name) for name in names]
comp = Composition(nuclei)
for i, nuc in enumerate(nuclei):
comp.X[nuc] = Y[i] * A[i]
return comp
def energy_release(dY):
"""return the energy release in erg/g (/s if dY is actually dY/dt)"""
enuc = 0.0
for i, y in enumerate(dY):
enuc += y * mass[i]
enuc *= -1*constants.Avogadro
return enuc
@jitclass([
("p_C12__N13", numba.float64),
("p_C13__N14", numba.float64),
("N13__C13__weak__wc12", numba.float64),
("p_N13__O14", numba.float64),
("p_N14__O15", numba.float64),
("p_N15__He4_C12", numba.float64),
("O14__N14__weak__wc12", numba.float64),
("O15__N15__weak__wc12", numba.float64),
])
class RateEval:
def __init__(self):
self.p_C12__N13 = np.nan
self.p_C13__N14 = np.nan
self.N13__C13__weak__wc12 = np.nan
self.p_N13__O14 = np.nan
self.p_N14__O15 = np.nan
self.p_N15__He4_C12 = np.nan
self.O14__N14__weak__wc12 = np.nan
self.O15__N15__weak__wc12 = np.nan
@numba.njit()
def ye(Y):
return np.sum(Z * Y)/np.sum(A * Y)
@numba.njit()
def p_C12__N13(rate_eval, tf):
# C12 + p --> N13
rate = 0.0
# ls09n
rate += np.exp( 17.1482 + -13.692*tf.T913i + -0.230881*tf.T913
+ 4.44362*tf.T9 + -3.15898*tf.T953 + -0.666667*tf.lnT9)
# ls09r
rate += np.exp( 17.5428 + -3.77849*tf.T9i + -5.10735*tf.T913i + -2.24111*tf.T913
+ 0.148883*tf.T9 + -1.5*tf.lnT9)
rate_eval.p_C12__N13 = rate
@numba.njit()
def p_C13__N14(rate_eval, tf):
# C13 + p --> N14
rate = 0.0
# nacrr
rate += np.exp( 15.1825 + -13.5543*tf.T9i
+ -1.5*tf.lnT9)
# nacrn
rate += np.exp( 18.5155 + -13.72*tf.T913i + -0.450018*tf.T913
+ 3.70823*tf.T9 + -1.70545*tf.T953 + -0.666667*tf.lnT9)
# nacrr
rate += np.exp( 13.9637 + -5.78147*tf.T9i + -0.196703*tf.T913
+ 0.142126*tf.T9 + -0.0238912*tf.T953 + -1.5*tf.lnT9)
rate_eval.p_C13__N14 = rate
@numba.njit()
def N13__C13__weak__wc12(rate_eval, tf):
# N13 --> C13
rate = 0.0
# wc12w
rate += np.exp( -6.7601)
rate_eval.N13__C13__weak__wc12 = rate
@numba.njit()
def p_N13__O14(rate_eval, tf):
# N13 + p --> O14
rate = 0.0
# lg06r
rate += np.exp( 10.9971 + -6.12602*tf.T9i + 1.57122*tf.T913i
+ -1.5*tf.lnT9)
# lg06n
rate += np.exp( 18.1356 + -15.1676*tf.T913i + 0.0955166*tf.T913
+ 3.0659*tf.T9 + -0.507339*tf.T953 + -0.666667*tf.lnT9)
rate_eval.p_N13__O14 = rate
@numba.njit()
def p_N14__O15(rate_eval, tf):
# N14 + p --> O15
rate = 0.0
# im05n
rate += np.exp( 17.01 + -15.193*tf.T913i + -0.161954*tf.T913
+ -7.52123*tf.T9 + -0.987565*tf.T953 + -0.666667*tf.lnT9)
# im05r
rate += np.exp( 6.73578 + -4.891*tf.T9i
+ 0.0682*tf.lnT9)
# im05r
rate += np.exp( 7.65444 + -2.998*tf.T9i
+ -1.5*tf.lnT9)
# im05n
rate += np.exp( 20.1169 + -15.193*tf.T913i + -4.63975*tf.T913
+ 9.73458*tf.T9 + -9.55051*tf.T953 + 0.333333*tf.lnT9)
rate_eval.p_N14__O15 = rate
@numba.njit()
def p_N15__He4_C12(rate_eval, tf):
# N15 + p --> He4 + C12
rate = 0.0
# nacrn
rate += np.exp( 27.4764 + -15.253*tf.T913i + 1.59318*tf.T913
+ 2.4479*tf.T9 + -2.19708*tf.T953 + -0.666667*tf.lnT9)
# nacrr
rate += np.exp( -6.57522 + -1.1638*tf.T9i + 22.7105*tf.T913
+ -2.90707*tf.T9 + 0.205754*tf.T953 + -1.5*tf.lnT9)
# nacrr
rate += np.exp( 20.8972 + -7.406*tf.T9i
+ -1.5*tf.lnT9)
# nacrr
rate += np.exp( -4.87347 + -2.02117*tf.T9i + 30.8497*tf.T913
+ -8.50433*tf.T9 + -1.54426*tf.T953 + -1.5*tf.lnT9)
rate_eval.p_N15__He4_C12 = rate
@numba.njit()
def O14__N14__weak__wc12(rate_eval, tf):
# O14 --> N14
rate = 0.0
# wc12w
rate += np.exp( -4.62354)
rate_eval.O14__N14__weak__wc12 = rate
@numba.njit()
def O15__N15__weak__wc12(rate_eval, tf):
# O15 --> N15
rate = 0.0
# wc12w
rate += np.exp( -5.17053)
rate_eval.O15__N15__weak__wc12 = rate
def rhs(t, Y, rho, T, screen_func=None):
return rhs_eq(t, Y, rho, T, screen_func)
@numba.njit()
def rhs_eq(t, Y, rho, T, screen_func):
tf = Tfactors(T)
rate_eval = RateEval()
# reaclib rates
p_C12__N13(rate_eval, tf)
p_C13__N14(rate_eval, tf)
N13__C13__weak__wc12(rate_eval, tf)
p_N13__O14(rate_eval, tf)
p_N14__O15(rate_eval, tf)
p_N15__He4_C12(rate_eval, tf)
O14__N14__weak__wc12(rate_eval, tf)
O15__N15__weak__wc12(rate_eval, tf)
if screen_func is not None:
plasma_state = PlasmaState(T, rho, Y, Z)
scn_fac = ScreenFactors(1, 1, 6, 12)
scor = screen_func(plasma_state, scn_fac)
rate_eval.p_C12__N13 *= scor
scn_fac = ScreenFactors(1, 1, 6, 13)
scor = screen_func(plasma_state, scn_fac)
rate_eval.p_C13__N14 *= scor
scn_fac = ScreenFactors(1, 1, 7, 13)
scor = screen_func(plasma_state, scn_fac)
rate_eval.p_N13__O14 *= scor
scn_fac = ScreenFactors(1, 1, 7, 14)
scor = screen_func(plasma_state, scn_fac)
rate_eval.p_N14__O15 *= scor
scn_fac = ScreenFactors(1, 1, 7, 15)
scor = screen_func(plasma_state, scn_fac)
rate_eval.p_N15__He4_C12 *= scor
dYdt = np.zeros((nnuc), dtype=np.float64)
dYdt[jp] = (
-rho*Y[jp]*Y[jc12]*rate_eval.p_C12__N13
-rho*Y[jp]*Y[jc13]*rate_eval.p_C13__N14
-rho*Y[jp]*Y[jn13]*rate_eval.p_N13__O14
-rho*Y[jp]*Y[jn14]*rate_eval.p_N14__O15
-rho*Y[jp]*Y[jn15]*rate_eval.p_N15__He4_C12
)
dYdt[jhe4] = (
+rho*Y[jp]*Y[jn15]*rate_eval.p_N15__He4_C12
)
dYdt[jc12] = (
-rho*Y[jp]*Y[jc12]*rate_eval.p_C12__N13
+rho*Y[jp]*Y[jn15]*rate_eval.p_N15__He4_C12
)
dYdt[jc13] = (
-rho*Y[jp]*Y[jc13]*rate_eval.p_C13__N14
+Y[jn13]*rate_eval.N13__C13__weak__wc12
)
dYdt[jn13] = (
-Y[jn13]*rate_eval.N13__C13__weak__wc12
-rho*Y[jp]*Y[jn13]*rate_eval.p_N13__O14
+rho*Y[jp]*Y[jc12]*rate_eval.p_C12__N13
)
dYdt[jn14] = (
-rho*Y[jp]*Y[jn14]*rate_eval.p_N14__O15
+rho*Y[jp]*Y[jc13]*rate_eval.p_C13__N14
+Y[jo14]*rate_eval.O14__N14__weak__wc12
)
dYdt[jn15] = (
-rho*Y[jp]*Y[jn15]*rate_eval.p_N15__He4_C12
+Y[jo15]*rate_eval.O15__N15__weak__wc12
)
dYdt[jo14] = (
-Y[jo14]*rate_eval.O14__N14__weak__wc12
+rho*Y[jp]*Y[jn13]*rate_eval.p_N13__O14
)
dYdt[jo15] = (
-Y[jo15]*rate_eval.O15__N15__weak__wc12
+rho*Y[jp]*Y[jn14]*rate_eval.p_N14__O15
)
return dYdt
def jacobian(t, Y, rho, T, screen_func=None):
return jacobian_eq(t, Y, rho, T, screen_func)
@numba.njit()
def jacobian_eq(t, Y, rho, T, screen_func):
tf = Tfactors(T)
rate_eval = RateEval()
# reaclib rates
p_C12__N13(rate_eval, tf)
p_C13__N14(rate_eval, tf)
N13__C13__weak__wc12(rate_eval, tf)
p_N13__O14(rate_eval, tf)
p_N14__O15(rate_eval, tf)
p_N15__He4_C12(rate_eval, tf)
O14__N14__weak__wc12(rate_eval, tf)
O15__N15__weak__wc12(rate_eval, tf)
if screen_func is not None:
plasma_state = PlasmaState(T, rho, Y, Z)
scn_fac = ScreenFactors(1, 1, 6, 12)
scor = screen_func(plasma_state, scn_fac)
rate_eval.p_C12__N13 *= scor
scn_fac = ScreenFactors(1, 1, 6, 13)
scor = screen_func(plasma_state, scn_fac)
rate_eval.p_C13__N14 *= scor
scn_fac = ScreenFactors(1, 1, 7, 13)
scor = screen_func(plasma_state, scn_fac)
rate_eval.p_N13__O14 *= scor
scn_fac = ScreenFactors(1, 1, 7, 14)
scor = screen_func(plasma_state, scn_fac)
rate_eval.p_N14__O15 *= scor
scn_fac = ScreenFactors(1, 1, 7, 15)
scor = screen_func(plasma_state, scn_fac)
rate_eval.p_N15__He4_C12 *= scor
jac = np.zeros((nnuc, nnuc), dtype=np.float64)
jac[jp, jp] = (
-rho*Y[jc12]*rate_eval.p_C12__N13
-rho*Y[jc13]*rate_eval.p_C13__N14
-rho*Y[jn13]*rate_eval.p_N13__O14
-rho*Y[jn14]*rate_eval.p_N14__O15
-rho*Y[jn15]*rate_eval.p_N15__He4_C12
)
jac[jp, jc12] = (
-rho*Y[jp]*rate_eval.p_C12__N13
)
jac[jp, jc13] = (
-rho*Y[jp]*rate_eval.p_C13__N14
)
jac[jp, jn13] = (
-rho*Y[jp]*rate_eval.p_N13__O14
)
jac[jp, jn14] = (
-rho*Y[jp]*rate_eval.p_N14__O15
)
jac[jp, jn15] = (
-rho*Y[jp]*rate_eval.p_N15__He4_C12
)
jac[jhe4, jp] = (
+rho*Y[jn15]*rate_eval.p_N15__He4_C12
)
jac[jhe4, jn15] = (
+rho*Y[jp]*rate_eval.p_N15__He4_C12
)
jac[jc12, jp] = (
-rho*Y[jc12]*rate_eval.p_C12__N13
+rho*Y[jn15]*rate_eval.p_N15__He4_C12
)
jac[jc12, jc12] = (
-rho*Y[jp]*rate_eval.p_C12__N13
)
jac[jc12, jn15] = (
+rho*Y[jp]*rate_eval.p_N15__He4_C12
)
jac[jc13, jp] = (
-rho*Y[jc13]*rate_eval.p_C13__N14
)
jac[jc13, jc13] = (
-rho*Y[jp]*rate_eval.p_C13__N14
)
jac[jc13, jn13] = (
+rate_eval.N13__C13__weak__wc12
)
jac[jn13, jp] = (
-rho*Y[jn13]*rate_eval.p_N13__O14
+rho*Y[jc12]*rate_eval.p_C12__N13
)
jac[jn13, jc12] = (
+rho*Y[jp]*rate_eval.p_C12__N13
)
jac[jn13, jn13] = (
-rate_eval.N13__C13__weak__wc12
-rho*Y[jp]*rate_eval.p_N13__O14
)
jac[jn14, jp] = (
-rho*Y[jn14]*rate_eval.p_N14__O15
+rho*Y[jc13]*rate_eval.p_C13__N14
)
jac[jn14, jc13] = (
+rho*Y[jp]*rate_eval.p_C13__N14
)
jac[jn14, jn14] = (
-rho*Y[jp]*rate_eval.p_N14__O15
)
jac[jn14, jo14] = (
+rate_eval.O14__N14__weak__wc12
)
jac[jn15, jp] = (
-rho*Y[jn15]*rate_eval.p_N15__He4_C12
)
jac[jn15, jn15] = (
-rho*Y[jp]*rate_eval.p_N15__He4_C12
)
jac[jn15, jo15] = (
+rate_eval.O15__N15__weak__wc12
)
jac[jo14, jp] = (
+rho*Y[jn13]*rate_eval.p_N13__O14
)
jac[jo14, jn13] = (
+rho*Y[jp]*rate_eval.p_N13__O14
)
jac[jo14, jo14] = (
-rate_eval.O14__N14__weak__wc12
)
jac[jo15, jp] = (
+rho*Y[jn14]*rate_eval.p_N14__O15
)
jac[jo15, jn14] = (
+rho*Y[jp]*rate_eval.p_N14__O15
)
jac[jo15, jo15] = (
-rate_eval.O15__N15__weak__wc12
)
return jac
We can now import the network that was just created and integrate it using the SciPy ODE solvers
import cno_test_integrate as cno
Integrating the network#
We can use the stiff ODE integration solvers that are part of SciPy to integrate this system now
from scipy.integrate import solve_ivp
import numpy as np
Initialize the thermodynamic conditions and initial composition. We express the composition as molar fractions, Y0.
rho = 150
T = 1.5e7
X0 = np.zeros(cno.nnuc)
X0[cno.jp] = 0.7
X0[cno.jhe4] = 0.28
X0[cno.jc12] = 0.02
Y0 = X0/cno.A
Now we integrate. We use the BDF method, since reaction networks are in general stiff
tmax = 1.e20
sol = solve_ivp(cno.rhs, [0, tmax], Y0, method="BDF", jac=cno.jacobian,
dense_output=True, args=(rho, T), rtol=1.e-6, atol=1.e-6)
Tip
You may need to change the relative (rtol) or absolute (atol) tolerances if you want to more accurately capture trace nuclei. Making them smaller will make the integrator work harder.
Plotting the results#
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
for i in range(cno.nnuc):
ax.loglog(sol.t, sol.y[i,:] * cno.A[i], label=f"X({cno.names[i].capitalize()})")
ax.set_xlim(1.e10, 1.e20)
ax.set_ylim(1.e-8, 1.0)
ax.legend(fontsize="small")
ax.set_xlabel("t (s)")
ax.set_ylabel("X")
fig.set_size_inches((8, 6))
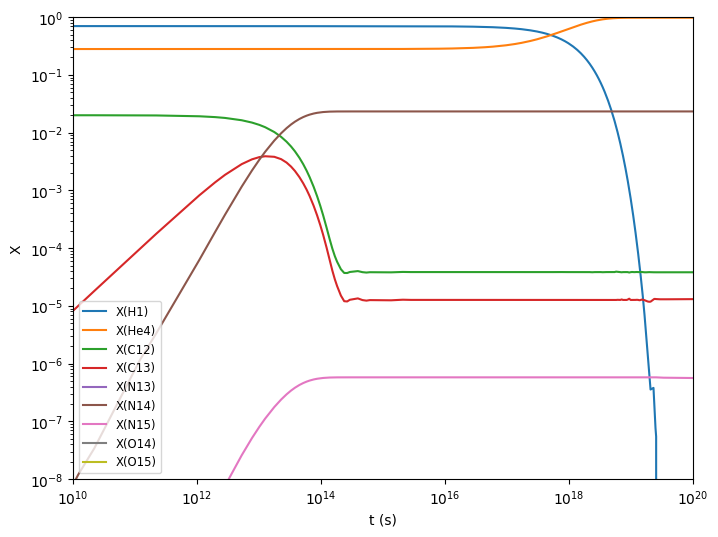
Energy release#
We can get the energy release from the change in molar abundances, \(\Delta Y\). This will be computed as:
\[\Delta E = -N_A \sum_i \Delta Y_i M_i\]
Here \(M_i\) is the mass of the nucleus \(i\) (this is tabulated in
the network as mass[]).
E = cno.energy_release(sol.y[:,-1] - Y0)
print(f"E = {E:20.10g}")
E = 4.510855593e+18
This result is in erg/g
We can compute the instantaneous energy generation rate as well,
\[\epsilon = -N_A \sum_i \frac{dY_i}{dt} M_i\]
epsilon = cno.energy_release(cno.rhs(0.0, Y0, rho, T))
print(f"epsilon = {epsilon:20.10g}")
epsilon = 117.7738358