The Electron-Positron EOS

The Electron-Positron EOS#

The ElectronEOS class managed an electron-positron equation of state, including the effects of relativity and degeneracy. It does this by directly computing the necessary Fermi-Dirac integrals.

Warning

The ElectronEOS can be slow because it is solving for the degeneracy parameter, \(\eta\), and doing all of the integrals at high precision.

Here we’ll explore the degeneracy parameter, \(\eta = (\mu - m_e c^2)/ (kT)\), where \(\mu\) is the chemical potential, as well as positron creation at low densities and high temperature.

import pynucastro as pyna

import numpy as np

Once we create an ElectronEOS, we can access the thermodynamics via the pe_state function.

es = pyna.eos.ElectronEOS()

We’ll create a grid of temperature and density and compute the thermodynamic quantities at each point.

Ts = np.logspace(4, 9, 26)
rhos = np.logspace(-4, 9, 66)

eta = np.zeros((len(rhos), len(Ts)))
n_e = np.zeros((len(rhos), len(Ts)))
n_pos = np.zeros((len(rhos), len(Ts)))

The only role composition plays in this EOS is determining the number density of electrons (assuming full ionization) via \(Y_e\).

comp = pyna.Composition(["he4"])
comp.set_equal()

for ir, rho in enumerate(rhos):
    for it, T in enumerate(Ts):
        state = es.pe_state(rho, T, comp, compute_derivs=False)
        eta[ir, it] = state.eta
        n_e[ir, it] = state.n_e
        n_pos[ir, it] = state.n_pos

Now we’ll make some plots

import matplotlib.pyplot as plt
from matplotlib import colors

Degeneracy parameter#

First, the degeneracy parameter. Since our grid of EOS points was coarse, we’ll use some interpolation to smooth it.

fig = plt.figure(constrained_layout=True)
ax = fig.add_subplot(111)
im = ax.imshow(eta.T, origin="lower",
               norm=colors.SymLogNorm(linthresh=0.01, vmin=-eta.max(), vmax=eta.max()),
               extent=[np.log10(rhos.min()), np.log10(rhos.max()),
                       np.log10(Ts.min()), np.log10(Ts.max())],
               interpolation="bilinear",
               cmap="RdBu")
ax.set_xlabel(r"$\log_{10}(\rho)$")
ax.set_ylabel(r"$\log_{10}(T)$")
ax.set_title(r"$\eta$")
fig.colorbar(im, ax=ax, orientation="horizontal")

<matplotlib.colorbar.Colorbar at 0x7f445e756890>
_images/a7b9c85459254dda9083552ac0a1a0473104511809a2c4f52baabe298729b500.png

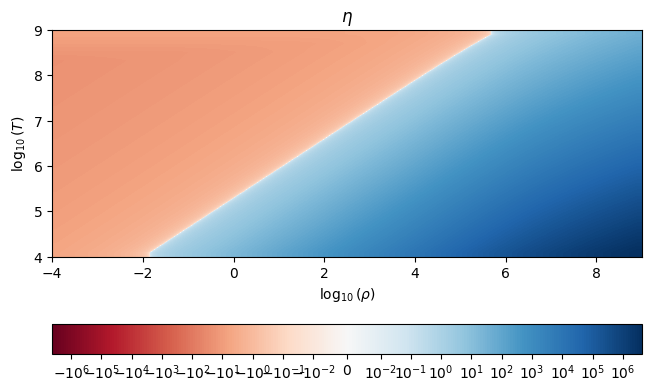
We see that at high temperatures, low densities, we are an idea gas (\(\eta \ll -1\)), while at high densities and low temperatures, we are very degenerate (\(\eta \gg 1\))

Electron-positron pairs#

At low density and very high temperatures (\(kT \sim m_e c^2\)), we can create electron positron pairs. Here we plot the fraction of positrons to the total number of electrons and positrons.

y = (n_pos / (n_pos + n_e))
y.min(), y.max()

(np.float64(0.0), np.float64(0.499999986135348))

fig = plt.figure(constrained_layout=True)
ax = fig.add_subplot(111)
im = ax.imshow(y.T, origin="lower",
               norm=colors.SymLogNorm(linthresh=1.e-5, vmin=1.e-50, vmax=0.5, clip=True),
               extent=[np.log10(rhos.min()), np.log10(rhos.max()),
                       np.log10(Ts.min()), np.log10(Ts.max())],
               interpolation="bilinear")
ax.set_xlabel(r"$\log_{10}(\rho)$")
ax.set_ylabel(r"$\log_{10}(T)$")
ax.set_title(r"$n^+ / (n^- + n^+)$")
fig.colorbar(im, ax=ax, orientation="horizontal")

<matplotlib.colorbar.Colorbar at 0x7f445c3d29d0>
_images/74cb2d742082c4adee510510ba6e18d7a5e0c80af19eb98fcc7e77bf5505f628.png

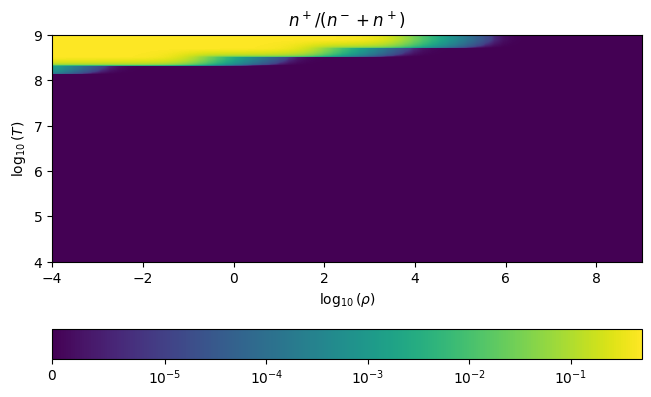
We see that we have nearly equal numbers of electrons and positrons at very low densities and high temperatures.

Contents